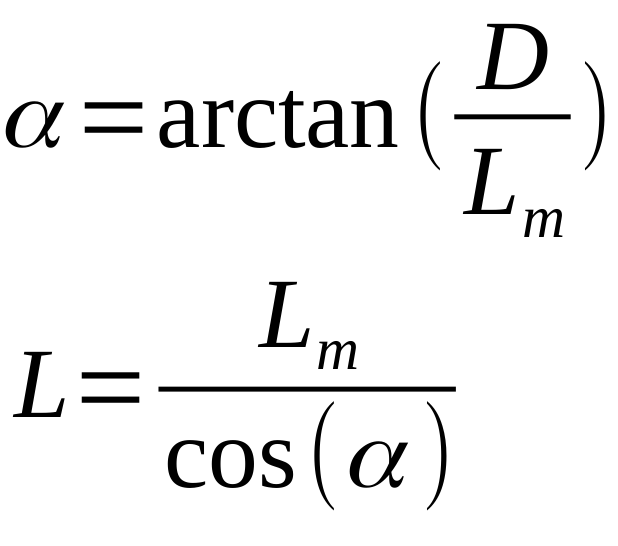Nella realtà per spostarsi fra i due punti individuati sulla mappa, solitamente, non è possibile procedere in linea retta ma si devono seguire sentieri e strade, che non hanno quasi mai un andamento rettilineo. Inoltre, occorre considerare che anche in presenza di un tracciato rettilineo fra i due punti, il percorso sul terreno presenta quasi sempre dei dislivelli da superare. In più, bisogna sempre ricordare che nessuna mappa, per quanto precisa, riporta tutte le svolte effettivamente presenti, ad esempio, in un ripido sentiero a tornanti.
Questo significa che la differenza tra la distanza misurata, soprattutto se in linea d'aria, e la distanza reale sul terreno può essere notevole e che, quindi, quella trovata deve essere considerata come puramente indicativa per valutare il percorso da compiere in termini di tempo e fatica.
Per valutare la distanza realmente esistente tra due punti presenti su di una mappa si possono utilizzare appositi strumenti, come scalimetro e curvimetro, oppure, in mancanza di questi, è possibile adottare alcuni accorgimenti. Le distanze così ottenute possono essere utilizzate per costruire il profilo altimetrico di un itinerario.
DISTANZA RETTILINEA O IN LINEA D'ARIA (DISTANZA PLANIMETRICA)
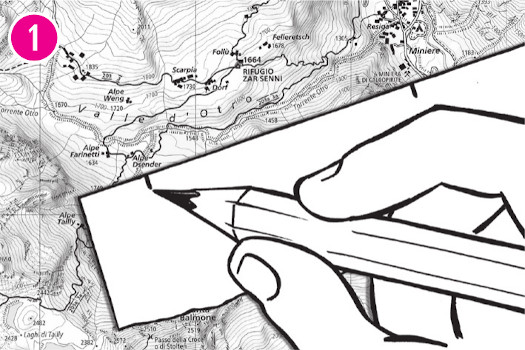
Utilizzare uno scalimetro della stessa scala della mappa oppure misurare con un righello (o segnare su un pezzo di carta) la distanza tra i punti di partenza e arrivo (1);
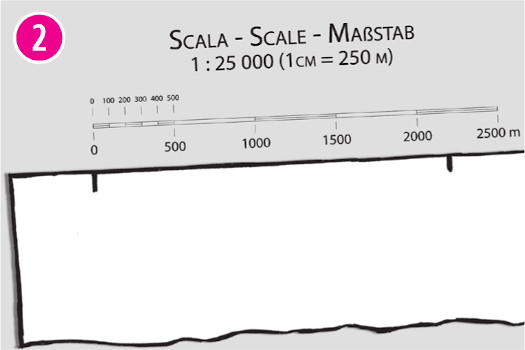
riportare sulla scala grafica la misura rilevata per visualizzare la distanza (planimetrica) in metri (2).
DISTANZA NON RETTILINEA
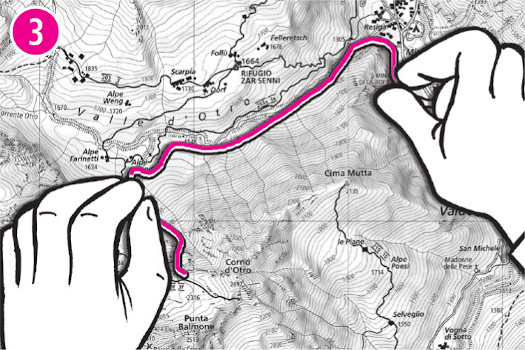
Utilizzare un curvimetro che abbia tra le scale possibili quella della mappa oppure sfruttare un filo (o la stringa dello scarpone) per ricalcare il percorso (3);
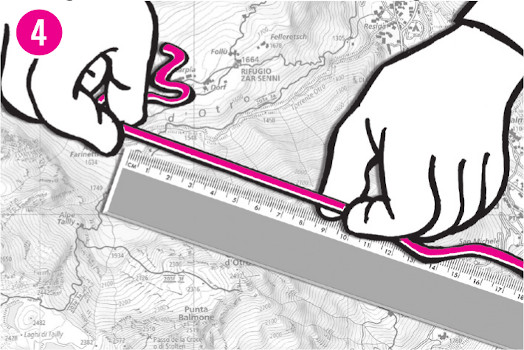
distendere il filo sulla scala grafica o su uno scalimetro per leggere direttamente il valore in metri oppure misurarlo con un righello e poi effettuare la conversione in metri in base alla scala numerica della mappa (4).
Approfondimento
Anche se la distanza misurata tra due punti P1 e P2 sulla carta è solo la distanza proiettata sul piano orizzontale, detta appunto distanza planimetrica, è possibile ottenere un'idea un po' più precisa sulla distanza reale da percorrere prendendo in considerazione anche il dislivello esistente tra le altitudini a cui si trovano i due punti.
Infatti, se si osserva il seguente semplice schema:
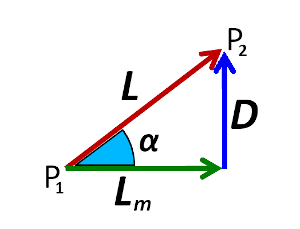
in cui Lm rappresenta la distanza planimetrica, ossia la lunghezza misurata sulla carta del percorso tra P1 e P2, D il dislivello tra le altitudini dei punti P2 e P1 e α l'angolo di inclinazione (→ Misurare pendenza e inclinazione), si può comprendere come sia possibile ottenere un'approssimazione della lunghezza reale L applicando il teorema di Pitagora:
![]()
oppure, sfruttando la trigonometria: